处理一类问题:
N个任务,M对二元组关系(x,y),求最小总花费,条件如下:
每个任务可以在机器A或机器B上完成,分别花费Ai、Bi。若x,y同时在A上完成,花费C1(x,y)。若x,y同时在B上完成,花费C2(x,y)。若x在A、y在B上完成,花费C3(x,y)。若x在B,y在A上完成,花费C4(x,y)。大概这种。
建模方法:
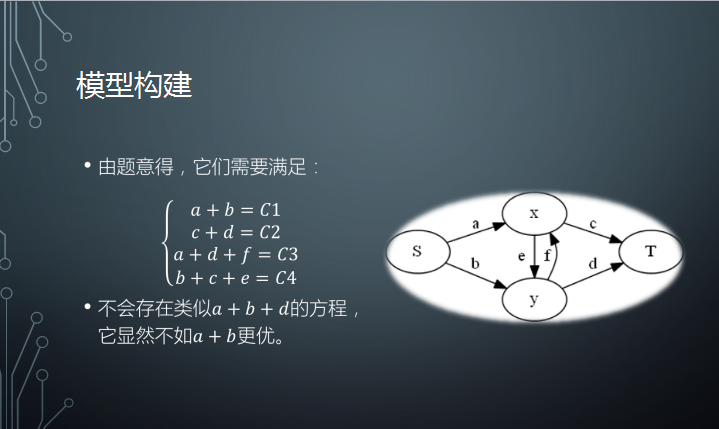
根据割集的定义列方程。
然后求解即可。
最后得到每条边的最终权值,由于每个这样的二元组都要最终做出选择。这样最后的最小割就包含了全局的所有的代价(就是加法交换律结合律就凑出来了)。
然后一些细节。

其实二元关系并不太常用,
对于比较容易解出答案的、某两个取不取会对答案造成影响的,就可以考虑这样建图。
是最小割建图的一个思路。
例题:
最大化收益的最小割,那么就把收益都算上,再减去为了符合题意而做出的最小的代价
直接列出方程:
a+b=0
a+f+d=3E
b+e+c=3E
c+d=2E
由于对称,直接e=f=2E,c=d=E,a=b=0即可。
这个题的好处是方程非常固定而且好解。
#include#define il inline#define reg register int#define numb (ch^'0')using namespace std;typedef long long ll;il void rd(ll &x){ char ch;bool fl=false; while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb); (fl==true)&&(x=-x);}namespace Miracle{const int N=1005;const int V=1005;const ll inf=0x3f3f3f3f3f3f3f3f;ll n,m,s,t;int cur[V];struct node{ int nxt,to; ll w;}e[2*(N*N*2+N*2)];int hd[V],cnt=1;int uu;void add(int x,int y,ll w){ e[++cnt].nxt=hd[x]; e[cnt].to=y; e[cnt].w=w; hd[x]=cnt; e[++cnt].nxt=hd[y]; e[cnt].to=x; e[cnt].w=0; hd[y]=cnt;}int d[V];ll dfs(int x,ll flow){ if(x==t) return flow; ll res=flow; for(reg i=cur[x];i&&res;i=e[i].nxt,cur[x]=i){ int y=e[i].to; if(d[y]==d[x]+1&&e[i].w){ ll k=dfs(y,min(res,e[i].w)); if(!k) d[y]=0; e[i].w-=k; e[i^1].w+=k; res-=k; } } return flow-res;}int q[V],l,r;bool bfs(){ memset(d,0,sizeof d); l=1,r=0; q[++r]=s; d[s]=1; while(l<=r){ int x=q[l++]; for(reg i=hd[x];i;i=e[i].nxt){ int y=e[i].to; if(!d[y]&&e[i].w){ d[y]=d[x]+1; q[++r]=y; if(y==t) return true; } } } return false;}ll E[N][N];ll ans;ll no[N];ll a[N];int main(){ rd(n); s=0,t=n+1; for(reg i=1;i<=n;++i){ rd(a[i]); add(i,t,a[i]); } for(reg i=1;i<=n;++i){ for(reg j=1;j<=n;++j){ rd(E[i][j]); ans+=E[i][j]; if(E[i][j]&&i